技術コラム

TECHNICAL
COLUMN

トップページ
技術コラム

診断の原理

本コラムではT-MCMAの診断の原理として、基礎理論であるMCSA（Motor Current Signature Analysis）とそこから発展した当社の診断技術について解説します。

MCSA　電動機の電流兆候解析

背景情報

1970年ごろ、世界の原子力発電所の動力源である原子炉内に設置された電動機を検査する技術が必要とされていました。これを受け、アメリカのテネシー州にあるオークリッジ国立研究所が、電動機の検査方法の研究開発を開始しました。また、ほぼ同時期に日本でも、当時の八幡製鉄所（現在の日本製鉄九州製鉄所八幡地区）が同様の研究開発に着手しています。

研究が進む中で、アメリカのオークリッジ国立研究所において、電動機のさまざまな異常状態で固定子の電流が変調することが発見されました。さらに、固定子と回転子間のエアギャップの変化や回転子バーの抵抗値変化、回転の変動、トルクの変動などが、固定子と回転子の間で相互作用する空間磁束線に影響を与え、逆起電力を通じて固定子電流が変調することが徐々に解明されていきました。

これにより、固定子電流の変調を用いて電動機の状態を解析する「MCSA（Motor Current Signature Analysis）」が考案されました。最初に実用化されたのは、電動機の回転子バーの破損を検出する方法です。現在では、MCSAは回転子の異常診断にとどまらず、回転子の静的・動的偏心、固定子鉄心の破損、巻き線の緩みや絶縁劣化、軸系のミスアライメント、ロータのアンバランス、軸受の損傷といった多岐にわたる異常を検出できる技術へと発展を遂げています。

1.1 誘導電動機の基本量

1.1.1誘導電動機の回転速度とすべり

　まず予備知識となる三相誘導電動機の基本量と計算例を確認しておきましょう。
同期速度は、固定子巻線の電流によって生じる回転磁界の回転速度 $N_0$ (rpm) となり、その周波数(Hz)値は同期回転周波数 $f_0=N_0/60$ (Hz)とともに次式で表されます。

N_0=\frac{60f_{line}}{(p/2)},\quad　f_0=\frac{N_0}{60}=\frac{2f_{line}}{p} \tag{1}

ここで、 $f_{line}$ は電源周波数(Hz)、 $p$ は電動機の極数を示します。電動機の最小極数はN極とS極の2極であり、式(1)分母は極数のペア数を示します。電動機回転子の回転速度（以下、電動機回転数）を (rpm)、その周波数(Hz)値は回転周波数 (Hz)とすると、誘導電動機のすべり率 $s$ は次式となります。

s=\frac{f_0-f_r}{f_0}=\frac{N_0-N}{N_0} \tag{2}

式(1)と(2)より誘導電動機の回転数 $N_ｒ$ および回転周波数は次式となります。

N_r=N_0(1-s),\quad　f_r=f_0(1-s)\tag{3}

そして、電動機のすべり回転数 $N_s$ (rpm)およびすべり周波数 $f_s=N_s/60$ (Hz)は次式となります。

N_s=N_0-N_r,\quad　f_s=f_0-f_r\tag{4}

（計算例）

電源周波数60Hzで駆動される4極電動機のすべり率が0.022として計算してみます。

電源周波数60Hzで駆動される4極電動機のすべり率が0.022として計算してみます。式(1)より同期回転周波数 $f_0$ (Hz)と同期回転速度 $N_0$ (rpm)は次のように求められます。

f_0=\frac{f_{line}}{(p/2)}=\frac{60}{4/2}=30\text{ (Hz)}

N_0=60f_0=60×30=1800\text{ (rpm)}

回転速度 $N_r$ (rpm)と回転周波数 $f_r$ (Hz)は式(3)より次のように求められます。

N_r=N_0(1-s)=1800(1-0.022)≈1760\text{ (rpm)}

f_r=f_0(1-s)=30(1-0.022)=29.34\text{ (Hz)}

電動機のすべり回転数 $N_s$ (rpm)と回転周波数 $f_s$ (Hz)は次のように求められます。

N_r=N_0-N_r=1800-1760=40\text{ (rpm)}

f_r=f_0-f_r=30-29.34=0.66\text{ (Hz)}

1.1.2極通過周波数

誘導電動機が $p$ 極で、すべり周波数が $f_s$ のとき、ある回転子バーが固定子巻線により生じる回転磁極を相対的に通過する周波数 $f_{pole}$ は次式となります。

f_{pole}=f_sp=(f_0-f_r)p\tag{5}

この周波数 $f_{pole}$ (Hz)を極通過周波数と呼びます。式(5)を式(1)、(3)を用いて次式のように表す場合もあります。

f_{pole}=\left(\frac{2f_{line}}{p})-2(1-s)\frac{f_{line}}{p}\right)p=2sf_{line} \tag{6}

この式から極通過周波数 $f_{pole}$ は磁極数 $p$ とは本質的に無関係であり、すべり $s$ と電源周波数 $f_{line}$ で表すことができます。
前文の計算例のデータを用いると、極通過周波数 $f_{pole}$ は次式となります。

f_{pole}=2sf_{line}=2×0.022×60=2.64\text{(Hz)}

2.1 電流信号解析の概要

　図1(a)に電動機固定子の実測電流信号の時系列波形(赤)を示しています。この例では電源周波数は $f_{line}=60$ Hzです。図1(a)で電源周波数 $f_{line}$ と同じ周波数の正弦波時系列波形（青）を重ね書きすると、実測電流の時系列波形は正弦波からわずかに歪んだ形状であることがわかります。MCSAではこのような微弱な電流変化を捉えています。
　この図1(a)の実測電流信号のFFT処理による振幅スペクトルを図1(b)に示しています。縦軸を線形目盛で示した図1(b)では、図1(a)の電流時系列波形の歪みにより予想される電源周波数 $f_{line}$ 以外の成分はほとんど判別できません。しかし、図1(c)のように縦軸を対数で示すと時系列波形の歪みによる電源周波数 $f_{line}$ 以外の成分が強調され、ノイズの他に電源周波数 $f_{line}$ の成分を基本として、両側に対称的なピークが現れます。このような成分（極通過周波数成分など）を側帯波といい、電動機・回転機械系の状態監視・診断の重要な情報となります。

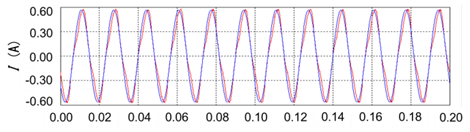
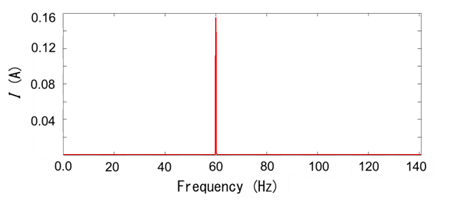
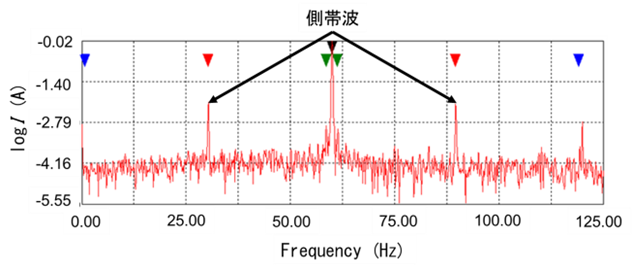
図1 実測電流信号の時系列波形とスペクトルの特徴（電源周波数 $f_{line}=60 \text{Hz}$ ）

　固定子巻線の電流には、電源から供給される駆動電流信号の他に、電動機回転機械系の様々な状態変化により生じる逆起電力による電流信号が含まれ、電流成分によって様々な周波数で現れます。また駆動電流信号と逆起電力による信号が相互に影響を与えることで振幅変調が起こります。

　例えば電動機に図2に示すような回転子が静的に偏心して上の方にエアギャップが大きく、下の方に小さい状態が生じると、固定子と回転子の磁界の作用のバランスが微妙に崩れ、結果として固定子巻線の電流に変化がもたらされます。同様に、他の回転機械系の異常の種類、例えば、回転子・固定子の電気抵抗の変化、負荷やトルクの変化によっても電動機の磁界に乱れが引き起こされ、固定子巻線の電流に特有の変化がもたらされます。
MCSAでは1.1で紹介したような基本量の情報をベースに電流変化による各周波数成分の振幅変調を捉え、機器の損傷・故障箇所を検出していますが、ここでは一例として回転子バー損傷の検出事例をご紹介します

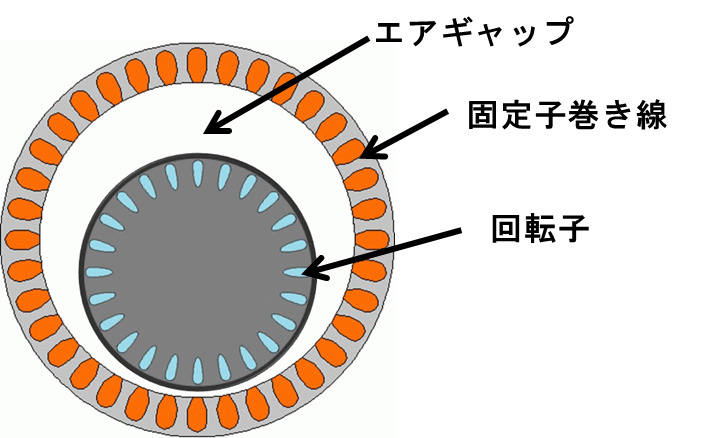
図2 回転子の偏心状態

2.2 MCSAと機器の損傷・故障箇所　「回転子バーの損傷」

　図３(a)のように損傷した回転子バーでは短絡環との継ぎ目の電気抵抗が非常に高い状態であると考えられます。そしてこのような損傷のある回転子バーを回転させると、固定子巻線が生じさせる回転磁界（回転電極）をこの回転子バーが通過するときに誘導電流が流れにくくなります。この周波数は極通過周波数 $f_{pole}$ となります。

　回転子バーの損傷が発生したときの固定子巻線電流信号のスペクトル特徴を図３(b)に示します。電源周波数が極通過周波数により変調されることで電源周波数 $f_{line}$ 成分の周りに $f_{band}$ の側帯波成分が生じ、側帯波の周波数は次式で表されます。

f_{band}=f_{line}\pm f_{pole}=f_{line}(1\pm2s)\tag{7}

ここで極通過周波数による側帯波成分の電流振幅値を $I_{pole}$ とすると、側帯波の大きさのdB値は図３(b)に示すように $20\text{log}(I_{pole}/I_{line})$ となります。この数値を用いた回転子バーの損傷度合の評価指標 $L_{pole}$ [dB]がよく用いられており次式となります。

L_{pole}=-20\text{log}\frac{I_{pole}}{I_{line}}=20(\text{log}I_{line}-\text{log}I_{pole})\tag{8}

この評価指標 $L_{pole}$ が48dB以下になると、回転子バーに損傷があると診断されます。

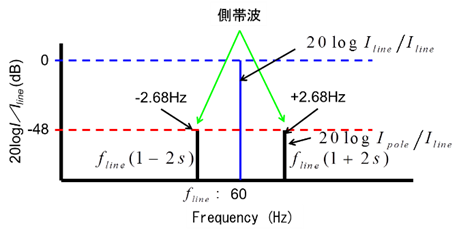
図３回転子バー損傷時の電流スペクトル

2.3 高調波解析

　電動機固定子電流信号周波数解析では、電源周波数を基本波とし、その整数倍( ：次数)を高調波と定義します。理想的な交流電源であれば、高調波成分は存在しませんが、実際の交流電源には高調波成分が必ず含まれます。そして、電源の品質が良くない場合や電動機固定子の絶縁劣化が発生している場合には、この高調波成分の含有率が高くなります。高調波成分が多く含まれると電動機の異常振動、電磁音や発熱などの問題を引き起こします。この高調波成分の特徴を調べることを高調波解析と呼びます。
　高調波解析に用いられる二つのパラメータを紹介すします。一つ目は最大高調波成分の含有率を評価する単調波比率 $IHD$ 、二つ目は全高調波成分の含有率を評価する全調波比率 $THD$ です。
　単調波比率 $IHD$ は高調波電流成分の最大値 $I_{hmax}$ と電源周波数成分 $I_{line}$ の比を取る次式を用います。

IHD=\frac{I_{hamax}}{I_{line}},\quad　I_{hmax}=\text{max}[I_2,I_3,\dots,I_N]\tag{9}

　全調波比率 $THD$ は高調波電流成分の2乗和の平方根を取り、これと電源周波数成分 $I_{line}$ との比を取る次式を用います。

THD=\frac{\sqrt{\sum_{n=2}^N I^2_n}}{I_{ine}}\tag{10}

　この高調波次数を上限 $N=30$ で算出しています。これらの単調波比率 $IHD$ と全調波比率 $THD$ は、電源品質の評価に加え、電動機固定子の絶縁劣化評価にも用いられます。

T-MCMAの診断技術

　T-MCMA（電流情報量診断システム）ではMCSAを基礎として電動機固定子電流信号に対して、時間領域と周波数領域の解析を行っています。
　解析結果から図４の計８種類のパラメータを算出し回転機械状態の簡易診断と劣化傾向の管理を行います。一般的に知られている $L_{pole}$ 以外のパラメータについてもこれまで実績から判定基準値を定めています。
　これらのパラメータの複合的な確認および精密解析によって図５のようにモータ本体だけでなくより広範な損傷・故障の検出を実現しています。