T-MCMAでは電流信号に対して、時間領域と周波数領域の解析を行っています。時間領域の解析結果としてKI、Irms、Iubを算出しています。周波数領域の解析結果としてLpole、Lshaft、Lx、IHD、THDを算出しています。
これら8種類のパラメータそれぞれの変化を確認したり、相関状態を確認することで回転機械の状態を各印することができます。
<目次>
8種類の診断パラメータ

KI
KIは回転機械系の状態全般を監視するパラメータです。
KIは測定された電流波形が正常な場合と比べてどの程度乱れているかを値にしています。
モータの駆動電流は機器の状態が正常な場合でノイズの影響も小さい場合は、限りなく正弦波に近いきれいな波形となります。このことから、測定されたモータ駆動電流の周波数と同じ周波数の正弦波の確率密度分布Rを求めます。このRと測定されたモータ駆動電流の確率密度分布TとのズレをKIとして算出しています。

例えば、測定された電流波形がこのようにきれいな場合は、KIは限りなく0に近い値となります。
逆に以下に示すように機器に異常が発生した場合は時間波形には脈動が確認され、確率密度分布にも違いが表れてきます。このような状態ではKIの値も大きくなります。(悪化)
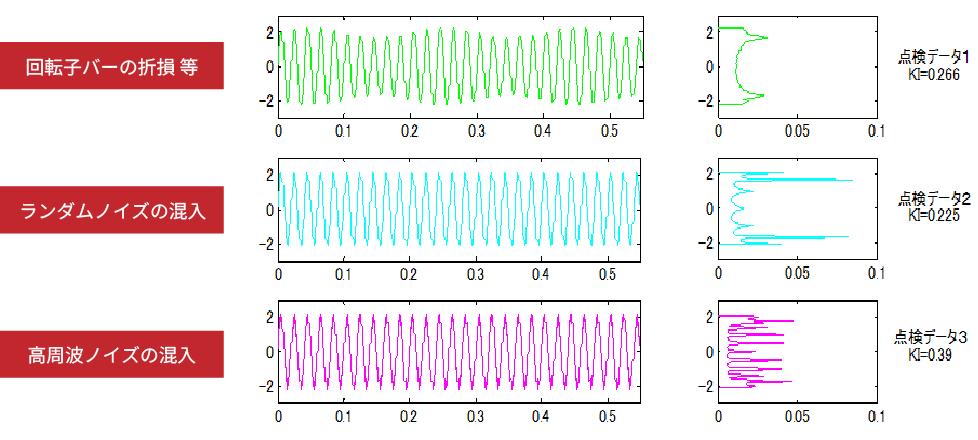
異常の信号が低周波の場合
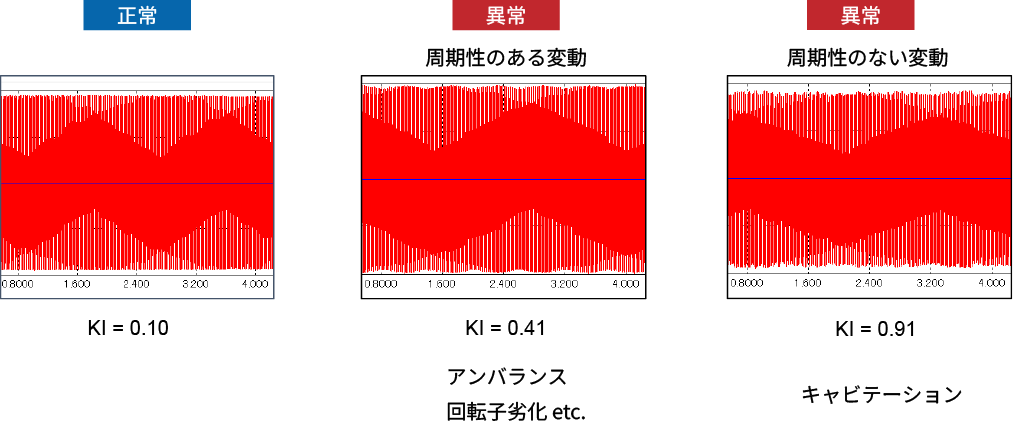
下図は測定された電流波形の数秒間分を枠の中に圧縮するようにして表示したものです。正常な場合は波形の極大値、極小値は大きく変化することはありませんが、低周波(電源周波数より低い周波数)を持った異常信号では変動が見られます。
例えば回転機械の回転数と異常発生時の周波数が密接に関係しているアンバランスや回転子劣化などの異常が発生した場合は周期性のある変動が見られます。またキャビテーションなどの流体異常や負荷変動が発生た場合は周期性のない変動が見られ、KIがより悪い値になる傾向があります。このようにKIは特に周期性を持たない異常信号に反応しやすいという特徴があります。
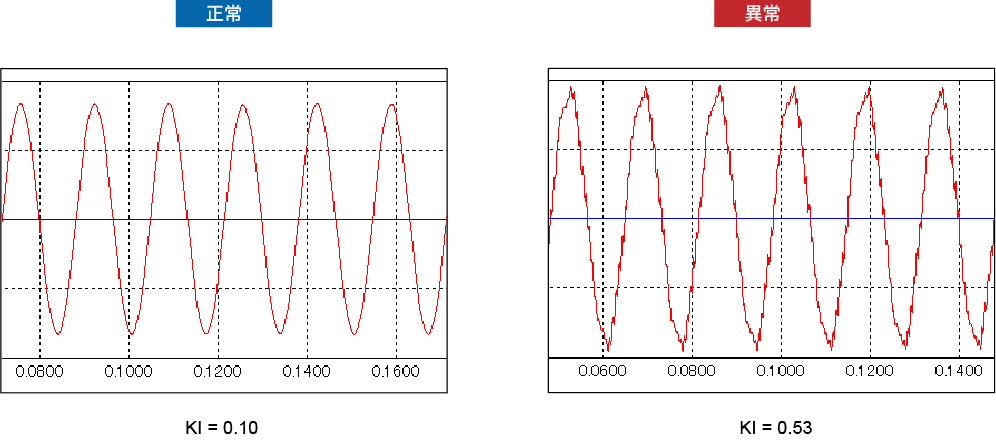
異常の信号が高周波の場合
異常の信号が高周波の場合、このように波形自体がギザギザと乱れます。このような波形は絶縁劣化が発生した際や高周波ノイズが混在した際に確認され、KIが悪化します。
インバータ駆動の機器の場合、キャリア周波数によっては波形が大きくギザギザしている場合があり、KIも大きくなるので注意が必要です。。
KIは波形が乱れる原因の特定はできませんが、機器の機械的状態や負荷の変動、電源的な異常状態といった回転機械系全般を監視するパラメータとして活用します。
Irms
Irmsは測定中(8秒間)の電流実効値です。回転機械の負荷や状態変動を監視するパラメータとして活用します。異常の例としては過負荷の発生が挙げられます。
Iub
Iubは三相電流のIrmsの大きさのズレを算出しています。電源品質、インバータの劣化、固定子の絶縁劣化などを監視するパラメータとして活用します。
IHD THD
どちらも電源周波数の高調波を監視するパラメータです。電源周波数(インバータ駆動の場合はその出力周波数)の2次~30次までの高調波の1次に対する割合を算出しています。IHDは2次~30次のうち最も強い信号の強さを示し、THDは2次~30次までのすべての高調波の1次の信号に対する強さを示しています。
電源品質やインバータ劣化、固定子の絶縁劣化などを監視するパラメータとして活用します。
Lpole
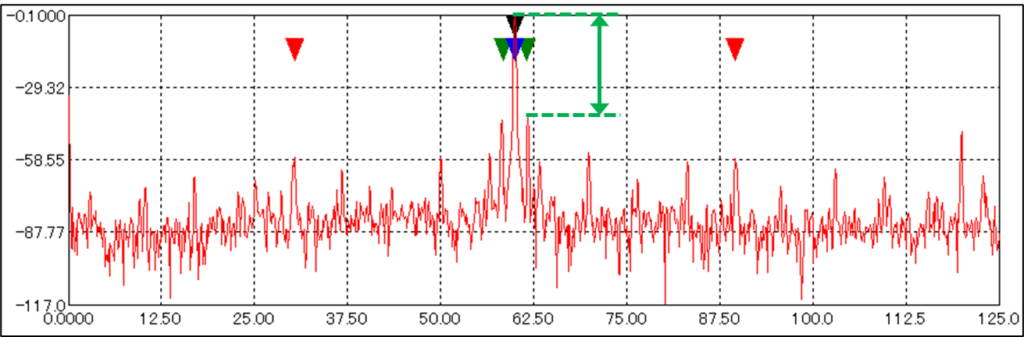
Lpoleは周波数領域のパラメータの一つです、電流の時間波形に対してFFT処理を行うと下図のようなグラフになりますが、中心の電源周波数周りにも側帯波が生じています。Lpoleはこのうち極通過周波数成分に着目し、その信号の強さの電源周波数に対する比を数値化したものです。側帯波の信号が強くなる、すなわち電源周波数との差が小さくなると悪化しているとされます。
モータの回転子の劣化状況を監視するパラメータとして活用します。
Lshaft
Lshaftは回転周波数成分に着目したもので算出方法はLpoleと同じです。
モータ接続軸系の芯ずれや曲がり、接触などの異常荷重を監視するパラメータとして活用します。
常時トルクが強くかかる現象、例えば低速軸の軸接触等では、対象軸が変速されていても監視可能です。
Lx
Lxは任意に参照する周波数成分を設定するものです。LpoleやLshaftは参照する周波数成分があらかじめ決まっていましたが機器構造などのあわせて個別に設定ができます。
例えばベルト駆動機器でベルトやプーリの状態を監視したい場合は次式で算出されるベルト通過周波数成分およびその次数成分にLxを設定します。

